what are the odds that the first football team to score will win a game?

Don't score just yet, Messi!

A look at the optimal times to score in a soccer game.

Picture from pexels.com

The game starts and your team scores the first goal on the 1st infinitesimal of the game. It sounds platonic, but did the odds of your opponent coming dorsum merely increase? What are your chances of winning the game and how do they compare if you lot were to score the game'south get-go goal in any other minute?

Using this Kaggle dataset (that includes detailed events from 9K games across some of Europe's height leagues from 2012 upwardly to 2017), I tried to sympathise the optimal time to score the first goal in a professional soccer game in guild to increase your chances of ultimately winning the game.

The first goal is one of the most important milestones in a soccer game. It tin give a boost of energy and confidence to the scoring team and add together pressure to the conceding team making them prone to concede again. One might deduce that scoring the get-go goal every bit quickly every bit possible is ideal, but the data suggests otherwise. Let'southward explore.

If you score early your squad can relax and perhaps fifty-fifty play ameliorate to score more goals. Scoring early on tin can also make the opponents immediately nervous hence more likely to brand more than mistakes that will allow your squad to score again.

But scoring early can besides be proficient for the opponents. Your team might relax because of the atomic number 82 and invite pressure from a adamant opponent, who knows that they have plenty of fourth dimension to improvement.

Correlation, not Causation

This analysis is intended as a showtime simple step toward understanding the correlation between the infinitesimal of the start goal and the probability of winning the game. Since this is only observation data no claims of causality tin be made.

The methodology

For each game in the dataset I take the minute that the outset goal was scored. Hence, this approach excludes from the dataset all games that ended a 0–0 draw. I then calculate the winner (or draw) of each game past comparison the number of goals that each squad scored.

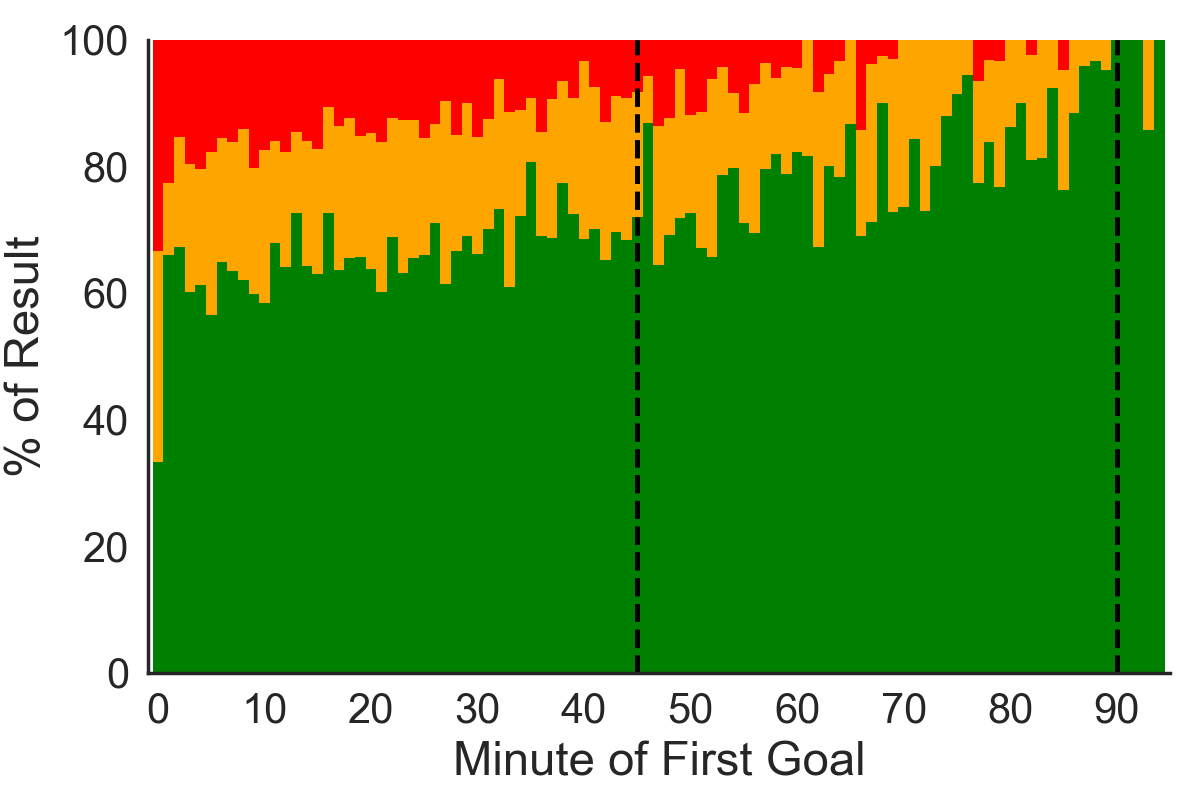
Finally, for each minute of the beginning goal I summate the percent of games that ended in a win, draw or loss of the team that scored that first goal. Here are the results.

Figure one. Probability of each result for each minute of the starting time goal. The result is from the perspective of the team that scored the outset goal. Legend: Green — Win, Orangish — Draw, Blood-red — Loss. The two dotted vertical lines indicate the half time (45) and full time (90) minutes.

Sample sizes

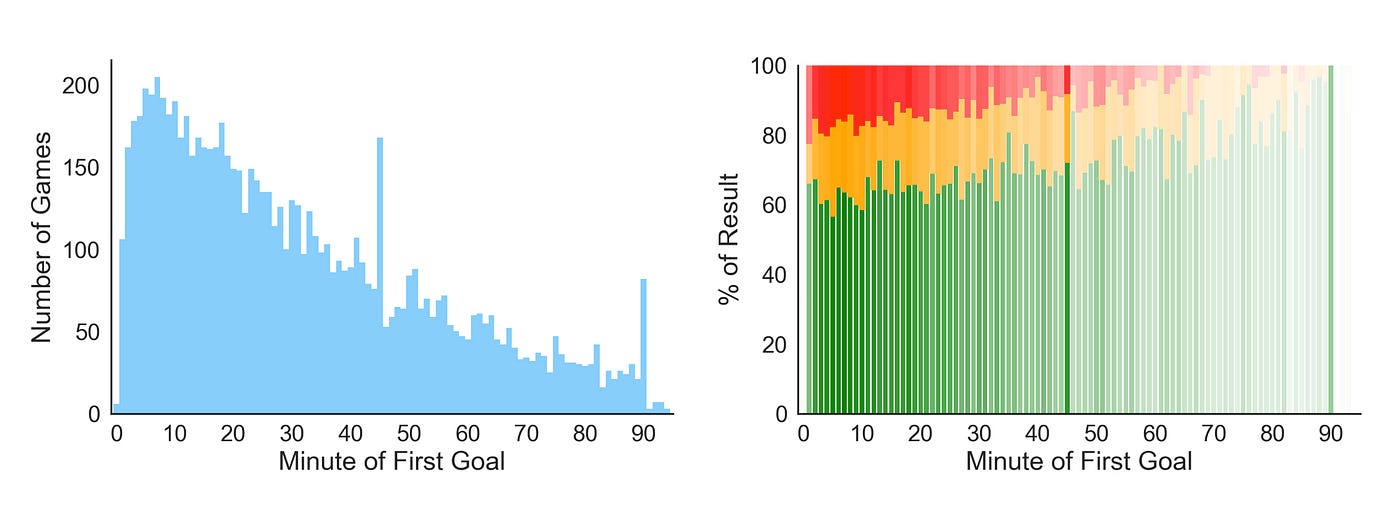
To increase confidence of the above distributions, I plotted the number of games that had their first goal scored in each possible infinitesimal (i.eastward., each bar's sample size). The more than games there are, the more than confidence we tin can take on the distribution of results. In an effort of clever data visualization I and so recreated the plot from Figure ane in a higher place and fabricated every bar'due south transparency proportional to its sample size. Hence, the bar for minute 20 is more opaque than minute 76 because there are more than games that had their outset goal scored on the 20th infinitesimal than the 76th infinitesimal (149 versus 39). The exact adding of the opacity is done by normalizing the range of the number of games to the [0,1] interval.

Figure 2. Left: The number of games in the dataset that had their first goal scored in each minute. Right: The distribution of results for each minute when the first goal was scored. Each bar's transparency is weighted according to plot on the left. The 2 bright bars are on the 45th and 90th minute (one-half time and full time).

Tidbits

1. On average, teams scoring the first goal of the game were 69% probable to win the game, 19% to describe and xi% to lose. Teams that scored the commencement goal in the first half had probabilities of 66%, 20% and 14%. Finally, teams scoring the first goal in the second one-half had probabilities of 79%, xvi% and 5%.
2. The probability that you will draw the game remains relatively stable no matter what minute you score the start goal. This is interesting because drawing requires the opponents to score at to the lowest degree ane goal (since your team scored the first goal) and hence 1 would look that the opponents are more likely to do that the earlier you score. This could indicate that the losing side shows "actress effort" to level the game if they are down but then play more cautiously so that they don't get scored upon once more.
3. Generally the afterwards you score the first goal of the game the college your chances of winning the game. And every bit Effigy 2 (left) shows there are substantially fewer outset goals scored as the game progresses. Conceivably, games standing for long durations without a goal can be an indication of 2 evenly matched teams. The likelihood of either of them scoring is thus lower.
4. The two points above indicate that the later y'all score the lower your probability of losing. Interestingly, your probability of drawing does not subtract the after yous score.
5. The slope of the linear regression is steeper for the 2nd half. Effigy 1 also shows that if you look at each half individually, the probability of a win increases by the minute in both halves. But it's increasing much faster in the 2d half.
6. The best fourth dimension to score is right after the halftime. Mayhap one of the nigh interesting things that jumps from the plots is that in that location is a substantive increase in your chances of winning the game if you score the first goal of the game right after the halftime. This could be caused by a number of reasons. Scoring too early in the game leaves the opponent with ample time to improvement. On the other manus, the longer you "wait" to score the less likely you are to score and more than likely to become scored upon. Hence, scoring correct subsequently halftime might be the perfect sweet spot. This finding can also be driven past the psychology of the opponent who showtime the second half and immediately get scored upon. Finally, the result can simply exist correlation: perchance the manager of the scoring team fabricated tactical changes and delivered a one-half-time speech that made the squad better which, in turn, drove both the probability of scoring every bit well as generally winning the game.

Conclusion

This is clearly a mostly theoretical analysis. The chances of winning the game if you score the first goal very tardily in the game are very high, merely that doesn't necessarily mean that a team should purposefully expect to score late, since that allows the opponents to score first. Perhaps one of the almost actionable insights of this assay is that the get-go few minutes of the 2d one-half are very crucial. Teams should be extra conscientious not to concede.

Nevertheless, this analysis provides an interesting data-driven perspective on whether you lot should actually relax next fourth dimension your favorite team scores very early in the game!

Exercise coaches suggest on key times to score? What does this analysis look like in other sports/eastward-sports?

Thanks for reading!

Y'all can find the jupyter notebook that produced all the analysis mentioned in this post here .

If y'all'd like more than soccer information assay, I as well wrote a post on whether a 2–0 lead is the "almost dangerous lead" in soccer. You lot can run into that post here .

P.South. A note on added (a.grand.a. extra) time

We find large spikes on the number of games that had their commencement goal score at the 45th and 90th minute. The spikes are so big that cannot reasonably be explained past only saying that the teams hurry more during those last minutes and produce more action.

My hypothesis is that those "minutes" are actually multiple minutes because they account for all added (aka injury aka extra) time. In soccer at the end of each half there are a few more added minutes played to business relationship for lost time during the bodily gameplay.

Figure 3. Number of events per game per minute

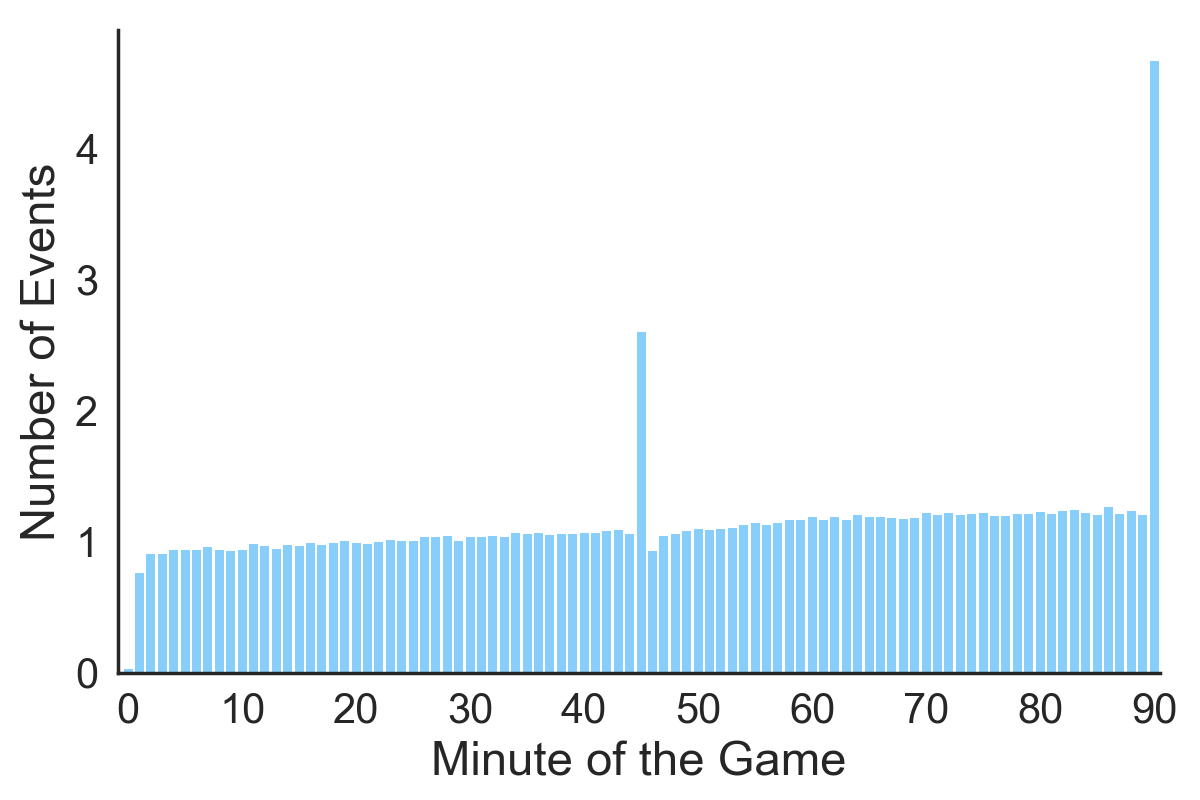
The number of added minutes is indicated past the referee and aims to capture any game-time that was lost due to fouls, goals or any other event that stopped the gameplay (but not the clock). Just that means that, on paper, the 45th minute (the last minute of the kickoff half) tin drag on for a few more than minutes. This is because 1 minute into added time is not the 46th minute, since the 46th minute is the first minute of the second one-half. An exploration of the number of events that happens per minute per game reveals a relatively steady trend. It besides shows that the number of events happening on the 45th minute is about 2.half dozen compared to around 1 in the minutes prior. This indicates that the average added time in the end of one-half time is effectually 2.6 minutes which sounds right. The same analysis shows an boilerplate of three.8 added minutes at full time which also sounds reasonable. Please let me know if you accept any other hypotheses.

Extra Time Edit: Home vs Away Team

Thanks to Rich Ford for his comment on what the analysis looks similar when cleaved downward by the team that scores the first goal, home or away. This is what information technology looks like.

The home team is consistently more likely to win the game when they score the offset goal compared to the away team when they score the first goal. If we see the probability of winning as a linear part of the time of scoring, the above insight can exist rephrased as the intercept of the linear model being higher for the home squad than the away team.

How the chances of winning change depending on the minute of the first goal, cleaved downward by the team that scored the first goal, home or away.

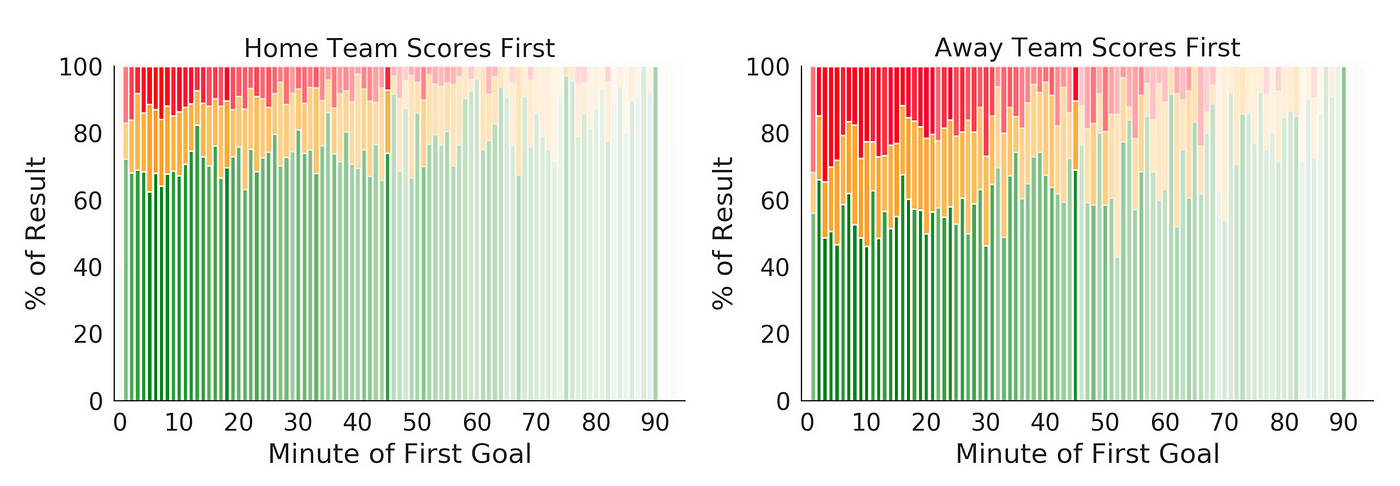
Only fifty-fifty though the intercept for the abroad team'south winning probability is lower to that of the home team, the away team'due south slope is steeper. This means that the later on the away team scores their chances of winning increase faster than that for the home team. Maybe this indicates a daze and pressure gene where the dwelling house squad finds itself behind on the scoreline in front of their own fans.

carterxvier1974.blogspot.com

Source: https://towardsdatascience.com/when-to-score-the-first-goal-to-beat-your-opponent-in-soccer-8d7b4e94035

Share this post